Cartesian Pump
The problem we discovered with ELSA is that, because the weight or buoyancy of the shuttle is spread over the area of the pumping tube, the actual force applied at the header tube is reduced.
What would happen if that force was applied at a point rather than over an area?
By modifying ELSA slightly, simplifying it, in fact, we could do just that. Consider the image below:
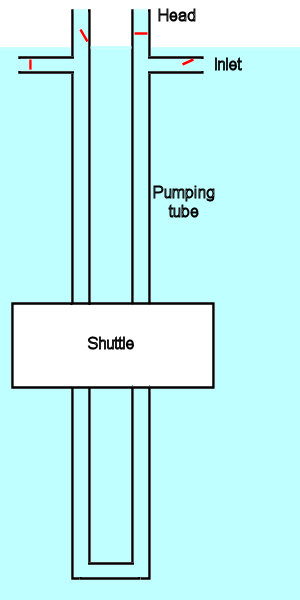
General layout
shuttle descending
Now we have the full 0.25kg weight/buoyancy acting on the header tube instead of 100th of the force that was applied by the shuttle inside a pumping tube.
The shuttle could use a magnetic coupling to a piston inside the pumping tube as illustrated below:
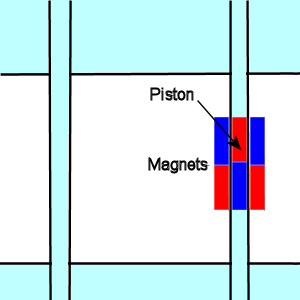
Section through shuttle
This design also reduces the friction involved in the pumping process since it reduces the contact area that existed between the shuttle and the pumping tube.
The shuttle could be much simplified by using the 'cartesian diver' principle. What would be required is to encase the entire pumping section inside a container that is closed at the top by a pressurising piston. Applying weight to the pressurising piston would increase pressure inside the container, which would compress the air inside the shuttle, causing it to descend. Lifting the weight from the top of the pressurising piston reduces the pressure, allowing the air in the shuttle to expand and the shuttle to become buoyant again. This is illustrated below:
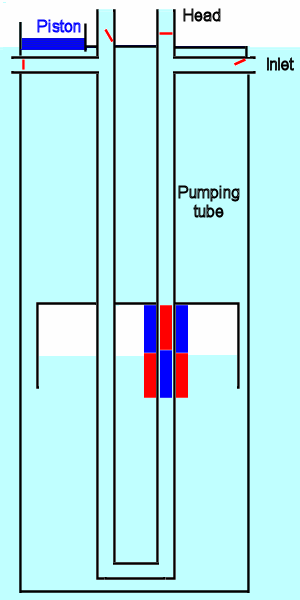
Cartesian pump
The above image shows pressure applied to the pressurising piston causing the shuttle to descend. This drives the pumping piston downwards, opening the inlet valve on the right and the header valve on the left whilst closing the header valve on the right and the inlet valve on the left.
Given a shuttle capacity of 3 litres and a weight of 1.25kg we want to increase the pressure inside the container until the air inside the shuttle compresses to 1 litre, giving us a negative buoyancy of 0.25kg. Since water is (effectively) incompressible we can simply pump water into the container to increase the pressure. We need to pump in 2 litres but how much weight would be required to do that?
Using the same dimensions that we used in the ELSA model we know that to compress 3 litres to 1 litre we need a weight of 200kg acting on an area of 100cm2 and we would have to compress it 20cm.. If we have sufficient height to compress it 40cm we could instead use a weight of 100kg acting over an area of 50cm2. Indeed, if we had a 2m head we could compress those 2 litres in a cylinder with an area of 10cm2 and a weight of 20kg.
This sounds hopeful until we consider the volume of water pumped on each stroke. Whereas ELSA pumped 198 litres per cycle (albeit to just under 2.5cm above water level) this version only pumps 1cm x 1cm x 10m x 2 = 2 litres (without accounting for pumping piston displacement) per cycle, this time to nearly 2.5m above water level.
Now we have less water at a greater head. Let's do an energy calculation for this configuration.
The head for the downstroke is 2.5m and the average head for the upstroke wil be 10m. The potential energy will be (1kg * 9.81m/s * 2.5m) + (1kg * 9.81m/s * 10m) = 122.625 joules; compared to a recompression requirement of 392.4 joules.
Where we gain on the height to which we can pump we lose on the volume that is pumped on each cycle.
Sadly, we are forced to conclude that however we go about capturing the energy from a buoyancy system we can never recover enough energy to recompress the shuttle.
Here is a little calculator that lets you try different combinations of shuttle size, weight and pump depth.
|
a. Shuttle diameter (cm) b. Uncompressed displacement (litres) c. Compressed displacement (litres) d. Pump depth (m) e. Shuttle weight (kg) |
g. Pressure at 0m = 0 times surface pressure. h. Displacement at 0m = 0 litres.
i. Shuttle area = 0cm2. j. Compressed shuttle height = 0cm. k. Uncompressed shuttle height = 0cm. l. Negative buoyancy = 0kg. m. Minimum positive buoyancy = 0kg. n. Maximum positive buoyancy = 0kg. o. Average positive buoyancy = 0kg. p. Downstroke energy = 0 joules. q. Upstroke energy = 0 joules. r. Total energy per cycle = 0 joules. |