An Introduction to ELSA

ELSA is a machine that uses buoyancy to raise water. It takes advantage of the fact that buoyancy depends on the displacement of an object relative to its weight. If you could change the weight of an object then you could make it rise or sink. Equally, changing the displacement of an object would also make it rise or sink.

If we add weight to an object to make it sink then we could use it to do work as it sinks. But we would have to do an equal amount of work to raise the weight back up again. If we compress an object then we change its displacement without changing its weight. Also when we compress something we have stored potential energy in it in the form of pressure (so long as it is elastic.) When we return the pressure to normal we get back the energy we used to compress it.

If we have a cylinder, open at one end, that fits snugly into a second cylinder, also open at one end, then we could push the first cylinder partially into the second and the closed cylinder that resulted (let's refer to it as a 'shuttle') would have a certain displacement. As we continue to push the second cylinder into the first the pressure inside would increase (so long as there is a good seal between them) and the displacement of the shuttle would decrease. If, when the first cylinder is partially inserted, the shuttle is just buoyant (it just floats) then when it is fully inserted it will sink (because its weight is greater than its displacement.)

Since it takes a certain amount of energy to compress the shuttle (because we are increasing the pressure inside) you would think that the only energy you could get back from it would be the same energy that it took to compress it. But we could take a long tube that the shuttle just fits into and we could place the tube vertically into a lake. Then as the shuttle sinks down the tube it will pump water down the tube until the shuttle reaches the bottom (so long as the top of the tube is just under the surface of the lake so that water can flow into it.) Not only that but once our shuttle reaches the bottom it still has potential energy stored as pressure inside it. That pressure can be used to expand the shuttle so that it becomes buoyant again. It will then rise up the tube, pumping water all the way until it reaches the top.

So we have pumped nearly (more on this below) twice the full volume of water in the tube for the mere cost of compressing the shuttle.

That is ELSA in a nutshell.

Many people will immediately say "That sounds like perpetual motion so it can't be right!" Let's examine the system in a more concrete fashion and see if it makes sense in terms of physics.

Let's work with a square shaped shuttle rather than a cylindrical one because the maths is easier.

The first thing you need to know is that a box that measures 10cm x 10cm x 10cm has a volume of exactly 1 litre (we will assume, for the moment, that the walls of the box are infinitely thin and infinitely rigid.)

The second thing you need to know is that normal air pressure is approximately 1kg/cm² or 1 bar at sea level. We need to be careful to distinguish between absolute pressure and gauge pressure since pressure gauges are usually set to read zero at sea level; they normally read a pressure difference.

The third thing you need to know is that fresh water weighs 1kg/litre.

Let's say our shuttle measures 30cm x 10cm x 10cm, so that it has a volume of 3 litres, and that it can be compressed down to 10cm x 10cm x 10cm, a volume of 1 litre.

Now let us put the compressed shuttle in a square tube that reaches down 10m into a lake. We'll call this the 'pumping' tube.

We can calculate the pressure on our shuttle at 10m depth by calculating the weight of water in a column directly above it. The area of the top of the shuttle is 10cm x 10cm and we could fit 10 x 10cm = 100 compressed shuttles into a column directly above it. The volume of water is 100 litres so the weight would be 100kg.

According to Boyle's Law pressure times volume gives a constant, so doubling the pressure will halve the volume. At sea level we had 1kg/cm² (from the weight of the atmosphere) and at 10m we add 1kg/cm², doubling the pressure to 2kg/cm². Half of 3 litres is 1.5 litres, which is what our shuttle will displace when it is allowed to expand at 10m.

At 20m we would have an additional 100kg acting on the shuttle, so 3 times the pressure at sea level. Thus the pressure at 20m will be 3kg/cm², exactly balancing the pressure inside our shuttle when it is compressed.

From this we can conclude that adding a weight of 200kg on top of the shuttle will compress it from 3 litres displacement to 1 litre.

Let's say our shuttle weighs 1.25kg. Once it is compressed to 1 litre it will sink down the tube, pushing down on the water underneath it.

When we first put the shuttle in the tube it will displace 1 litre in the top of the tube, so let's ignore that 1 litre. On its way down the tube the shuttle will pump 99 litres of water out of the bottom of the tube.

At the bottom of the tube the shuttle will also be displacing 1 litre so let's disregard that litre also. Our system releases the ends of the shuttle and it expands to 1.5 litres. Since it weighs 1.25kg and displaces 1.5 litres it will rise up the tube. On the way up it will pump 99 litres of water out of the top of the tube.

So in a complete cycle our shuttle has pumped 198 litres of water but it pumped 99 of those litres down to 10m and 99 of those litres up to the surface. Neither of these is very useful to us.

So let's make our system a little more sophisticated: We'll close the top and the bottom of the pumping tube and add a second tube that is 12m x 1cm x 1cm to the side of it, extending 2m above the surface of the lake. We'll call this second tube the 'header' tube. We'll also add a few valves so that one valve lets water from the lake into the top of the pumping tube when the shuttle is going down and lets water flow into the header tube when the shuttle is going up. We will have a similar valve that allows water to flow from the bottom of the pumping tube into the header tube when the shuttle is going down and allows water to flow from the lake into the bottom of the pumping tube when the shuttle is going up.

The volume of the 2m of header tube that extends above water level is 0.2 litres (200cm x 1cm x 1cm.)

When compressed, our shuttle displaces 1 litre. Since it weighs 1.25kg it will exert a force of 0.25kg on the water underneath it. We hope that this will be able to support 0.25kg of water in our header tube but when considering forces we have to consider the area they are acting on. Our shuttle has an area of 100cm² so we have to divide the force by 100 to find the force per cm². Thus the force from the shuttle is 0.25 / 100 = 0.0025kg/cm². When we apply that to the 1cm x 1cm area of the header tube we find that it will only support 2.5cc of water and we have to shorten the header tube so that it has a height (or 'head') of, say, 2cm above water level. We could make it 2.5cm but then the weight of water in the header tube would exactly match the pressure from the shuttle and no water would get pumped.

When the shuttle reaches the bottom it expands to 1.5 litre displacement and exerts a force of 0.25kg on the water above it. This is exactly the opposite situation as we had when the shuttle was descending except that this time the shuttle will continue to expand as it rises because the pressure of the water reduces as it gets closer to the surface. Consequently the pressure acting on the header tube will also increase but we have no way to take advantage of this with our current setup.

At the end of the cycle we would have 198 litres stored at a head of 2cm.

198 litres weighs 198kg and that is not enough to recompress the shuttle (since we need 200kg for that.) The head is 2cm but we have to compress our shuttle 20cm to bring it back to 3kg/cm² and a displacement of 1 litre.

We could use a lever with a ratio of 10:1 to increase the distance over which the water could act but that would require 10 times the force (2000kg) acting upon it and we are already short of what we need.

Perhaps the way to succeed is to find a way to capture the extra force produced by the difference in pressure from 10m to 0m. We can calculate how much force that would be by taking the average of the force at 10m and the force at 0m. We already worked out the force at 10m: 0.0025kg/cm². At 0m our shuttle will have expanded back to 3 litres so it will be exerting a force of 3 - 1.25 = 1.75kg or 0.0175kg/cm². The average is then (0.0025 + 0.0175) / 2 = 0.01kg/cm²; a head of 10cm.

So now we would have a theoretical 99 litres stored at a 2.5cm head and 99 litres stored a 10cm head. We are taking a best case example here, ignoring the fact that the head will have to be slightly less in order for the shuttle to be able to pump at all.

Energy can be calculated using the formula mass x gravity x height so the potential energy stored by the shuttle on a complete cycle is (99kg * 9.81m/s * 0.025m) + (99kg * 9.81m/s * 0.1m) = 19.4238 + 97.119 = 116.5428 joules.

Converting the force required to compress the shuttle to energy we get: 200kg * 9.81m/s * 0.2m = 392.4 joules.

The shuttle produces just 30% of the energy required for recompression.

Sadly, after all of this effort, ELSA will not work. But at least we now know that and, I hope you will agree, we also know why it won't work.

But don't loose hope yet. There is a way to overcome the hydraulic disadvantage of a pumping cylinder having 100 times the area of the header cylinder. Take a look at my Cartesian Pump page.

Please direct any discussion to this topic on www.overunity.com

Many people have asked me, "What would a system look like to keep the shuttle compressed until it reaches the bottom of the pumping tube?" and "How would recompression work?"

Take a look at the image below:

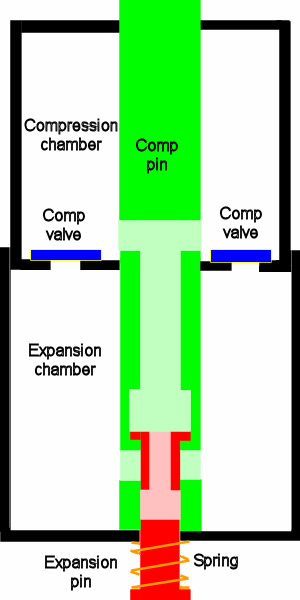
The shuttle is divided into two chambers, a compression chamber and an expansion chamber.

To recompress the shuttle you would pull up on the top of the compression pin (green) whilst holding the top of the compression chamber. The expansion chamber would be pulled up into the compression chamber (because the bottom of the expansion chamber is fixed to the bottom of the compression pin.) This would force air from the expansion chamber through the compression valves (blue) into the compression chamber. When the shuttle is fully compressed the compression valves would be forced closed by the pressure in the compression chamber.

When the shuttle reaches the bottom of the pumping tube its weight will cause the expansion pin (red) to move upwards until the channel in the expansion pin (light red) and the channel in the compression pin (light green) align. Air will then flow from the compression chamber into the expansion chamber until the shuttle has expanded to a point where it is buoyant. Once the shuttle is buoyant it will begin to rise and the spring (orange) will push the expansion pin back down, closing the airway in the compression pin.

This particular design will only work to approximately double the displacement of the shuttle. In order to triple it (which is necessary for ELSA to work) you could extend the compression pin and add a second expansion chamber outside the first with an airway between the two. This might cause some problems with leakage from the compression pin since its air channel would extend out of the top of the compression chamber when the shuttle is compressed, so I am working on a better design for this.